Union-Find, also known as Disjoint Set Union (DSU), is a set of algorithms used to solve the dynamic connectivity problem. This problem involves maintaining connections or relationships between a set of N objects. Two fundamental operations in Union-Find are:
- Union: This operation connects two objects.
- Find: This operation checks whether there exists a path connecting two objects.
Problem Statement
Consider a collection of objects and various connections between them. Union-Find helps us determine if two objects are connected directly or indirectly through a chain of connections.
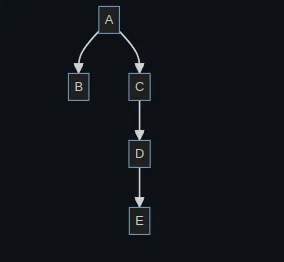
Consider these Graphs:

connection(A, F): The connection query returns False as there is no direct or indirect connection between A and F.
connection(C, E) The connection returns True. Although there C and E are not connected directly. But there exist a path from C to E.
union(A, C): This will create a connection between A and C. Giving us this graph:
Applications of Union Find
- Social Networks: Modeling connections between friends or users in a social network.
- Image Processing: Managing pixel connectivity in digital photos for tasks like image segmentation.
- Symbol Tables: Keeping track of variable names in a program.
When programming, its convenient to name objects from 0 to N-1. Then we use integers as array index.
Mathematical Properties Maintained by Union-Find
Union-Find maintains the following mathematical properties for the "is connected to" relationship, treating it as an equivalence relation:
- Reflexive: Any object is connected to itself (p is connected to p).
- Symmetric: If object p is connected to object q, then object q is also connected to object p.
- Transitive: If p is connected to q and q is connected to r, then p is connected to r, forming a transitive relationship.
Connected Components
Connected components are a set of objects that are mutually connected. When any two objects within a connected component are connected, it implies that there are no external objects or connections linking to them. In other words, connected components represent self-contained groups of objects with no connections extending beyond these groups.
Implementation
Design a Data Strucutre for Union Find
- Number of objects N can be huge.
- Number of operations M can be huge.
- Find Queries and Union commands may be intermixed.
class UF:
# Initialize UF data structure with N Objects(0 to N-1)
def __init__(self, N: int):
# Add connection between p and q
def union(self, p: int, q: int) -> None:
pass
# Are p and q in the same component
def connected(self, p: int, q: int) -> bool:
pass
# Component identifier for p(0 to N-1)
def find(self, p: int) -> int:
pass
# Number of components
def count() -> int:
pass
Quick Find Implementation
Data Structure
- Integer array of size
N. - Interpretation:
pandqare connected if and only if they have thesame id.
Consider these graphs representing our 10 objects:

This is how our ID array will look like:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 8 | 8 | 0 | 0 | 1 | 8 | 9 |
Based on the array:
- 0, 5, and 6 are a connected component.
- 1, 2, and 7 are a connected component.
- 3, 4, and 8 are a connected component.
- 9 is its own component.
Find
Check if p and q have the same ID. If yes, they are a connected component.
Union
To merge components containing p and q, change all entries whose ID equals id[p] to id[q]. This can be a problem if we have large number of objects.
Code in Python for Quick Find
class QuickFind:
def __init__(self, N):
# Set ID of each object to itself
self.id = []
for i in range(N):
id[i] = i
# Check if p and q are in the same component
def isConnected(self, p, q):
return self.id[p] == self.id[q]
# Change all entries with id[p] to id[q]
def union(self, p, q):
pid = self.id[p]
qid = self.id[q]
for i in range(len(self.id)):
if self.id[i] == pid:
self.id[i] = qid
Cost Model for Quick Find
Number of array access(for read or write):
- Initialize: N
- Union: N
- find: 1
Quick-find defect: Union is too expensive.
Example Takes N^2 array access to process of N union commands on N objects It’s quadratic. Quadratic algorithms don’t scale with technology.
Quick Union Implementation
Data Structure
- Integer array of size
N. - Interpretation:
id[i]is the parent ofi. - Root of
iisid[id[id[.....id[i]....]]].
Consider these graphs:
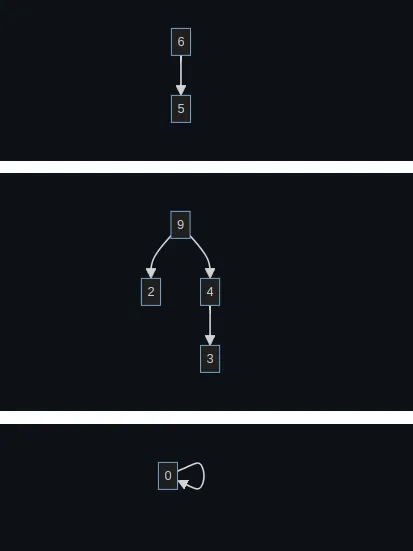
This is how our ID array will look like:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 9 | 4 | 9 | 6 | 6 | 7 | 8 | 9 |
Find Operation
Check if elements p and q have the same root. To find the root of an element, like 3, you would use: id[id[id[3]]], which results in 9.
If the roots are the same, p and q are part of the same connected component.
Union Operation
To merge components containing p and q, set the id of p’s root to the id of q’s root. This operation involves changing one entry in the array, unlike Quick Find, which requires changing all entries where the root equals p.
Cost Model for Quick Union
Number of array accesses (for read or write):
- Initialize: N
- Union: N
- Find: N
Defect of Quick-Union: Trees can get tall, making the find operation potentially expensive (up to N array accesses).
Improvements in Quick Union ==> Weighted Quick Union
- Modify Quick Union to avoid tall trees by keeping track of the size of each tree (number of objects).
- Balance by linking the root of the smaller tree to the root of the larger tree.
Data Structure
- Uses the same structure as quick union but maintains an additional size array to count the number of objects in the tree rooted at each node.
- Find operation remains the same as in quick union.
- Modify union operation to:
- Link the root of the smaller tree to the root of the larger tree.
- Update the size array.
Runtime
- Find: Time proportional to the depth of p and q.
- Union: Constant time given the roots. Depth of any node is at most logN.
Examples of operation counts:
- For N = 1,000: ~10 operations.
- For N = 1,000,000: ~20 operations.
- For N = 1,000,000,000: ~30 operations.
Quick Find:
- Union runtime: N
- Connected runtime: Constant
Quick Union:
- Union runtime: N
- Connected runtime: N
Weighted Quick Union:
- Union runtime: LogN
- Connected runtime: LogN
Further Performance Improvement ==> Path Compression
After computing the root of p, set the id of each examined node to point directly to that root.
- Two-pass implementation: Add a second loop to the root method to set the
id[]of each examined node to the root. - Simple one-pass variant: Make every other node in the path point to its grandparent, thereby halving the path length.

